数量关系必备八大思维

【导读】。更多招考资讯，备考干货，笔试资料，辅导课程，时政资料欢迎关注四川事业单位招聘考试网获取。

四川教师备考交流群：533419591   | 备考题库：国培教师APP   

数量关系必备八大思维

一、倍数思维

所求量为正整数，且具备倍数特性，可考虑倍数思维。

【例1】一些员工在某工厂车间工作，如果有4名女员工离开车间，在剩余的员工中，女员工人数占九分之五，如果有4名男员工离开车间，在剩余的员工中，男员工人数占三分之一。原来在车间工作的员工共有（  ）名。

A.36                           

B.40                           

C.48                           

D.72

倍数思维：所求量的是总员工数，其满足条件：，由此可得：总-4=9n，那么代入选项仅B选项满足条件，故本题答案为B项。

【例2】某公司三名销售人员 2011年的销售业绩如下：甲的销售额是乙和丙销售额的 1.5倍，甲和乙的销售额是丙的销售额的5倍，已知乙的销售额是56万元，问甲的销售额是：（  ）

A. 140万元

B. 144万元

C. 98万

D. 112万元

倍数思维：要求的是甲的销售额，其满足条件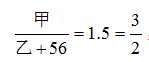：，由此可得：甲=3n，那么代入选项仅B选项满足条件，故本题答案为B项。

二、方程思维

存在等量关系时，可根据等量关系列方程求解。

【例1】去年光明中学的学生比涌泉中学学生的2倍多54人，今年光明中学增加了20人。浦泉中学减少了8人，则光明中学的学生比涌泉中学的学生的4倍少26人。去年光明中学比涌泉中学的学生多（  ）人。

A.115  

B. 120  

C. 130  

D.125

方程思维：题干中存在明显的等量关系，可设去年涌泉中学学生x人，那么去年光明中学学生（2x+54）人。根据题意：（2x+54）+20=4（x-8）-26，解得x=66，那么2x+54-x=120。故本题答案为B项。

三、代入思维

缺乏思路或求解困难，可考虑代入排除。

【例1】王同学将压岁钱200元按一年期存入某储蓄所，到期后取出100元用来购买衣服，剩下的100元和应得的利息又全部按一年期存入，若存款的年利率保持不变，这样到期后可得本金和利息共132元，请问这种存款的年利率为（ ）。

A.1/5

B.1/10

C.1/11

D.1/7

代入思维：设年利率为x，根据条件可列方程：[200（1+x）－100]（1+x）=132。求解方程困难，考虑代入选项，B项最好计算，故先代入B项检验，验证正确，故本题答案为B项。

【例2】AB两地相距12千米，船只往返AB两地需4.5小时，已知水速为2千米/小时，若船只自身速度不变，那么船只静水速度是（ ）千米/小时。

A.3

B.4

C.5

D.6

代入思维：设船速为x，可得方程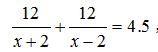：，求解分式方程困难，考虑代入选项，代入验证D选项符合条件，故本题答案为D项。

四、特值思维

题干变量不影响结果，可考虑设置特值。

【例1】从一瓶浓度为20%的消毒液中倒出2/5后，加满清水，再倒出2/5，又加满清水，此时消毒液的浓度为：

A.7.2%

B.3.2%

C.5.0%

D.4.8%

特值思维：题干中未提及任何与溶液、溶剂、溶质质量相关的数据，说明溶液质量不影响结果，可设溶液质量为100份，那么最初溶质为100×20%=20份。经过两次操作之后，溶质还剩：20×（1-2/5）×（1-2/5）=7.2份，溶液质量不变，所以最终浓度为7.2%。故本题答案为A项。

【例2】木匠加工2张桌子和4张凳子共需要10个小时，加工4张桌子和8张椅子需要22个小时。问如果他加工桌子、凳子和椅子各10张，共需要多少小时？

A.47.5     

B.50     

C.52.5     

D.55

特值思维：设加工桌子、凳子、椅子分别需要x小时、y小时、z小时，根据题中等量条件可得方程：①2x+4y=10；②4x+8z=22。显然这是不定方程，且未知量x、y、z可以非整数，那么存在无限组x、y、z满足条件，而所求量10（x+y+z）为固定结果，可知x、y、z取值不影响结果。取x=0，可得y=2.5，z=2.75，所以10（x+y+z）=52.5。故本题答案为C项。

五、常识思维

所求量必然满足生活常识。

【例1】某工厂11月份工作忙，星期日不休息，而且从第一天开始，每天都从总厂陆续派相同人数的工人到分厂工作，直到月底，总厂还剩工人240人。如果月底统计总厂工人的工作量是8070个工作日（一人工作一天为1个工作日），且无人缺勤，那么，这月由总厂派到分厂工作的工人共多少人：（  ）

A.2    

B.60     

C.240     

D.298

常识思维：总厂人数必然比分厂人数多，所以派出的工人应少于240人，且每天有派人，故派出人数需大于30人。故本题答案为B项。

【例2】一家四口人年龄之和为149岁，其中外公年龄、母亲年龄以及两人的年龄之和都是平方数，而父亲7年前的年龄正好是孩子年龄的6倍。问外公年龄上一次是孩子年龄的整数倍是在几年前？（  ）

A.2

B.4

C.6

D.8

常识思维：母亲年龄是平方数，必然是25岁或36岁。16岁的母亲不符合社会主义主流价值观；根据母亲和外公年龄和为100岁，可知49岁的母亲不可能有51岁的外公。验证母亲年龄25岁时，外公75岁不合题意，所以母亲年龄为36岁，外公年龄为64岁。再设7年前孩子x岁，那么：6x+7+x+7=49，解得x为5，今年孩子年龄12岁。代入选项，D项符合条件。故本题答案为D项。

六、居中思维

溶液混合时，混合浓度在大小浓度之间

【例1】现有一种浓度为15%的盐水30千克，如果用50千克浓度更高的盐水和它混合，混合后的盐水浓度将大于20%，而小于35%。据此可知，后加入的盐水的浓度（假设浓度为x）范围是：（  ）

A.23%＜x＜47%

B.15%＜x＜35%

C.15%＜x＜23%

D.23%＜x＜50%

居中思维：混合后的盐水浓度大于20%，混合前一种盐水浓度15%，那么另一种盐水浓度必然大于20%，故答案锁定A、D项。代入D项进行验证，若盐水浓度为50%，此时可算出混合盐水浓度约37.5%，超过35%，不合题意。故本题答案为A项。

七、极限思维

利用极限条件限制取值范围

【例1】有粗细不同的两支蜡烛，细蜡烛的长度是粗蜡烛长度的2倍，点完细蜡烛需要1小时，点完粗蜡烛需要2小时，有一次停电，将两支蜡烛同时点燃，来电时，发现两蜡烛所剩长度一样，则此次停电共停了多少分钟？（  ）

A.10分钟      

B.20分钟        

C.40分钟       

D.60分钟

极限思维：选项中最长60分钟，细蜡烛已燃烧完毕，明显不行；再考虑30分钟，细蜡烛剩一半，等于初始状态粗蜡烛的高度，必然比现在的粗蜡烛高，因此时间在30-60分钟之间，故本题答案为C项。

【例2】汽车以每小时54千米的速度笔直地开向峭壁，驾驶员按一声喇叭，6秒后听到回声，已知声音的速度是每秒340米，问听到回声时，汽车离峭壁的距离是多少米？（  ）

A.975

B.1020

C.1065

D.1155

极限思维：声音跑的路程为：340×6=2040米，路程的一半是1020米，再考虑汽车自身的速度，那么现在汽车离峭壁的距离应小于1020米，故本题答案为A项。

八、形式思维

几何问题常有固定计算公式，可借鉴公式形式选答案。

【例1】将一个边长为1的木质正方体削去多余部分，使其成为一个最大的木质圆球，则削去的体积为多少？

A.π/6    

B.1-π/6   

C.π²/6     

D.1-π²/6

形式思维：削去的体积必然是：正方体体积减去球体体积，所以锁定B、D两项，而几何公式中π从来都是一次方，没有出现过平方，故本题答案为B项。